Reliability
Problem 2
Reliability is the probability that a service or product/component will perform according to expectations.
Total Reliability=The product of all reliabilities
To solve the reliability problem of the engine, we sketch a diagram of the details.
Diagram Component
The reliability of the ten parts in the series is given by:
R_s=(R_1 )(R_2 )(R_3 )(R_4 )(R_5 )(R_6 )(R_7 )(R_8 )(R_9 )(R_10 )
Since all the components have equal reliabilities (0.998), the above expression can be reduced to:
R_s=R^10
The average reliability of each component R is 0.998.
Replacing R with 0.998 and solving for it will yield the total reliability of the engine.
R_s=〖0.998〗^10
R_s=0.980
Therefore, the reliability of the engine is 0.980.
Are you interested in an original copy of the “Reliability assignment”? Contact us.
Problem 10
Reliability is the probability that a service or product/component will perform according to expectations.
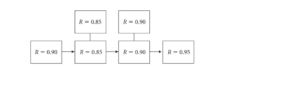
System Components
This system has four components, with two of these components containing a backup.
The backup components can be combined to form a single part.
The total reliability of the second component can be calculated as follows:
component reliability=original+backup
The original reliability in the system is marked with an arrow.
0.85+0.85(1-original)
R_2=0.85+0.85(1-0.85)
=0.9775≅0.98
The reliability of the second component is 0.98
The total reliability of the third component can be calculated as follows:
component reliability=original+backup
The original reliability in the system is marked with an arrow.
=0.90+0.90(1-original)
R_2=0.90+0.90(1-0.90)
=0.99
The reliability of the second component is 0.99
After eliminating the backup systems, the final design can be represented as follows:
Final System
The total reliability of this system can be calculated by multiplying the reliabilities of the components making up the system, including backups.
Total Reliability=The product of all reliabilities
R_s=(R_1 )(R_2 )(R_3 )(R_4 )
R_s=0.9×0.9775×0.99×0.95
R_s=0.83
Therefore, the reliability of the system is 0.83
Other Related Post: Capital Market In a “perfect world.”
References
Reid, R. D., & Sanders, N. R. (2016). Operations Management, Binder Ready Version: An Integrated Approach. John Wiley & Sons.
ORDER A PLAGIARISM-FREE PAPER HERE
We’ll write everything from scratch
Question 
Total Quality Management: Reliability
Complete the following problems in your textbook:
Reliability
- Problem 2 on page 179.
- Problem 10 on page 180.
For help completing these problems, see the Solved Problems on pages 178–179.
Complete the order form and upload all of your files, including any instructions, rubrics, or other materials provided by your instructor. 
Complete the order payment after filling in the order form. We’ll receive your order and assign it to a writer.
The assigned writer will complete your paper and forward it to our Editing Team for review and approval.
Once approved by the editor, the completed paper will be uploaded to your account for you to download, review and approve.