Need Help With This Assignment?

Let Our Team of Professional Writers Write a PLAGIARISM-FREE Paper for You!

SUBMIT YOUR ASSIGNMENT

Mathematics, Pages: 1

Multiple Ways to Teach a Concept – Equivalent Fractions, Prime and Composite Numbers

Multiple Ways to Teach a Concept – Equivalent Fractions, Prime and Composite Numbers

Concept #1 Example Problem
Defining prime and composite numbers. Which of the given numbers is a prime or composite number?

8, 5, 12
Video link found Online Video Link you created
https://www.youtube.com/watch?v=ydm2cxacPIM https://youtu.be/VTWiDiHh1AA
Solving the problem using the Online video method Solving the problem using your own video method
Prime numbers are numbers that only have two factors; 1 and itself, while composite numbers are numbers that have more than two factors excluding 1 and itself.

8 = 1,2,4,8; therefore, 8 is a composite number

5= 1 and 5; therefore, 5 is a prime number

12 = 1, 2, 3, 4, 6, 12; therefore, 12 is a composite number

 Numbers that only have two dividers and two factors; namely, itself and 1 are called prime numbers.

Numbers with more than two dividers and factors; except for itself and 1 are called composite numbers.

8:

1×8=8

8×1= 8

2×4= 8

8÷1= 8

8÷2= 4

8÷4= 2

8÷8= 1

Therefore, 8 is a composite number.

5:

1×5= 5

5×1= 5

5÷1= 5

5÷5= 1

Therefore, 5 is a prime number.

12:

1×12= 12

2×6= 12

3×4= 12

4×3= 12

6×2= 12

12×1= 12

12÷1= 12

12÷2= 6

12÷3= 4

12÷4= 3

12÷6= 2

12÷12= 1

Therefore, 12 is a composite number.

 

Concept #2 Example Problem
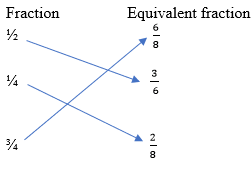
Equivalent Fractions Match the following fractions to their equivalent fractions

Fraction                 Equivalent fraction

½                              6⁄8

¼                                 3⁄6

¾                               2⁄8

 

 
Video link  found Online Video Link you created
https://www.youtube. com/watch?v=W72eW83rrC8 https://youtu.be/DAb9OWMbVyc
Solving the problem using the Online video method Solving the problem using your own video method
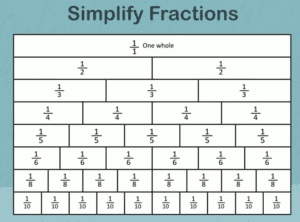
Equivalent fractions are equal fractions.

 

½ = 2 quarters and 3 sixths, therefore, ½ = 3⁄6

¼= 2 eighths, therefore, ¼= 2⁄8

¾= 6 eighths, therefore, ¾= 6⁄8

 

 

 Equivalent fractions are fractions with varying denominators and numerators with similar proportions.

Multiplication can be used to determine the equivalent fractions.

3 × (½) =  therefore, ½ =   3⁄6

2 × (¼) =  therefore, ¼ = 2⁄8

2 × (¾) = , therefore, ¾ = 6⁄8

ORDER A PLAGIARISM-FREE PAPER HERE

We’ll write everything from scratch

Question 

Assessment Description
Creating videos allows teachers to save hours of repetitive teaching. Students also thrive if they can view a concept multiple times. It is important as a teacher that you can create short videos for your students to help them through the class.

Equivalent Fractions, Prime and Composite Numbers

Equivalent Fractions, Prime and Composite Numbers

Directions:

Use the tables below to do the following:

  • Select two concepts that were covered in Topics 3 and 4 of the course. Then, select one example problem for each concept you selected.
  • Search the internet to find a video that teaches each of your selected concepts.
  • Create your own videos that teach the concepts in a different way than the videos you found on the internet. (You will need to upload your video to a video-sharing site that provides a link that you can paste below. Your video should not be “searchable” within the video-sharing site. If you upload your video to YouTube, select the “unlisted” option so it is not searchable. Ensure that others can access and view your linked video prior to submitting it to the LMS.)
  • Solve your selected example problem twice, using the method employed in the video you found online and using the method employed in the video you created. (Please show all work. (Hint: If you solve the problem on a piece of paper, just take a picture and copy and paste it into a Word document. You do not have to type to solve the answer.)
Concept #1 Example Problem
Video link found Online Video Link you created
Solving the problem using the Online video method Solving the problem using your own video method

 

Concept #2 Example Problem
Video link  found Online Video Link you created
Solving the problem using the Online video method Solving the problem using your own video method